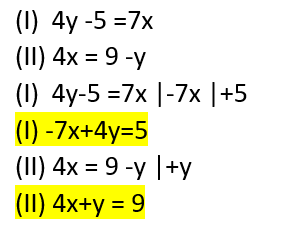
Um ein Gleichungssytem im Taschenrechner zu lösen müssen die Gleichungen gleich aufgebaut sein.
Das x und das y müssen auf der linken Seite  vor dem = stehen die Zahlen ohne x und y auf der rechten Seite bevor man diese in den Taschenrechner kann.

Haben wir nun eine Gleichung die falsch aufgebaut ist muss diese wie links gezeigt umgeformt werden. Zahlen werden durch das umgekehrte Vorzeichen auf die andere Seite gebracht. 

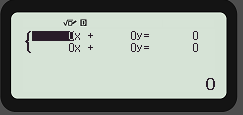
1. Zuerst wird das Menü durch die Menütaste geöffnet

2. Hier navigieren wir mit den Cursortasten zu Feld A:
Gleichung/Funkt

3. Mit der =-Taste bestätigen wir die Auswahl

4.Für unser Beispiel benötigen wir das Gleichungssystem und wählen dies durch das Drücken der Taste 1 aus.
Bei Falschauswahl kann mit der Cursortaste nach links zurücknavigiert werden

5. Da wir 2 Unbekannten haben, nämlich x und y wählen wir hier 2 aus.
Bei einer Falschauswahl muss die ganze Auswahl erneut gestartet werden.

6. Jetzt könnt ihr eure Formel eingeben.
Die Eingabe erfolgt Kästchenweise.
Zuerst wird das x eingegeben und mit = bestätigt.
Die Auswahl springt dann automatisch ins nächste Feld.
Mit den Pfeiltasten lässt sich durch diese Formel ebenfalls
navigieren.

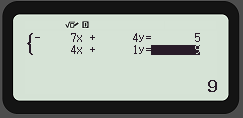
In unserem Beispiel haben wir die Formeln
(I) -7x+4y=5
(II)4x+y=9
Das y wird mit 1 angegeben das man in der normalen Schreibweise einfach weggelassen würde aber für die Berechnung mit dem Taschenrechner braucht.

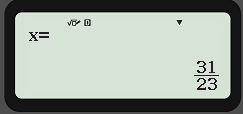
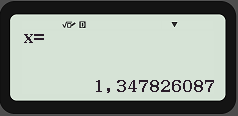
Mit dem fertigstellen der Formel und dem Anschließenden drücken der =-Taste wird auch schon die Lösung für X angezeigt.
Möchte man zwischen einem Dezimalem und einem Bruch wechseln kann man dies durch den Tastendruck S<=>D machen.
Mit anschließenden Drücken auf die =-Taste wird das Ergebnis für Y angezeigt und mit erneuten Drücken der Taste kann man wieder Änderungen an der Formel vornehmen. 

Angabe der Lösung

Die Angabe der Lösung erfolgt als L= {(x|y)} in unserem obigen Beispiel also L={(1,348|3,609)} oder die Angabe als Bruch. Um die volle Punktzahl für die Aufgabe zu erhalten wird immer die Lösungsmenge wie hier gezeigt benötigt.

Es gibt zwei Spezialfälle beim Lösen von linearen Gleichungssystemen. Zum Einen gibt es Gleichungssysteme die sich nicht lösen lassen und welche die unendlich viele Lösungen haben.

Keine Lösung

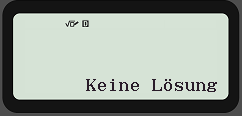
(I) -3x + y = -1
(II) 9x -3y = -14
Bei keiner Lösung verschwindet beim Berechnen entweder das x oder das y und damit ist das Gleichungssystem unlösbar.
Die Lösungsmenge wird in so einem Fall mit L={  } angegeben

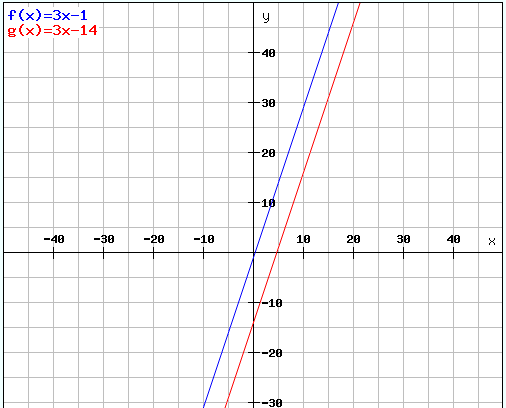
Grafisches Verständnis
(I) y=3x-1
(II) y=3x-14

Zeichnet man die oben berechneten Formeln erkannt man recht schnell das die beiden Geraden sich parallel zueinander befinden. Es ist daher unmöglich, dass es einen Schnittpunkt der beiden Geraden geben kann.

Unendlich viele Lösungen

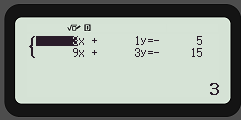
(I) 3x + y = -5
(II) 9x +3y = -15
Hierbei ist es egal welche Zahlen man für x und y einsetzt, denn jede Zahl ist möglich. Eine der beiden Formeln muss nach y umgestellt werden um die Lösungsmenge richtig angeben zu können.
Das mache ich hier mit der Gleichung I.
(I) 3x + y = -5 | -3x
(I) y=-3x-5
Die Lösungsmenge lautet L={(x|y)    | y=-3x-5}

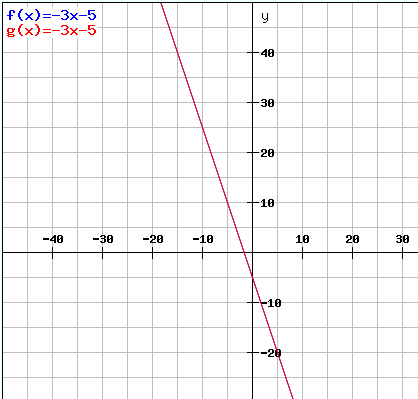
Grafisches Verständnis
(I) y=-3x-5
(II) 9x+3y = -15 |:3
(II) 3x+y = -5 | -3x
(II) y = -3x-5
Wie man allein schon an den beiden Gleichungen erkennen kann sind sie identisch sie schneiden sich also auf jedem Punkt an dem man versucht sie zu lösen.